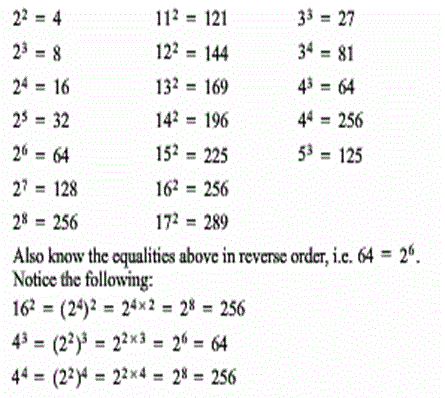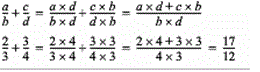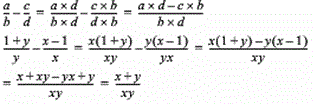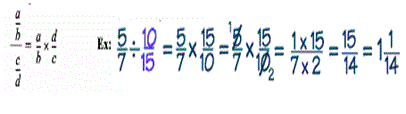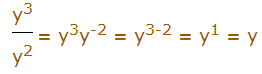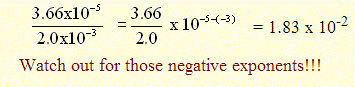Important concepts for GMAT Mathematics - Part 1
Numbers
Fractions to decimals

Powers of Numbers
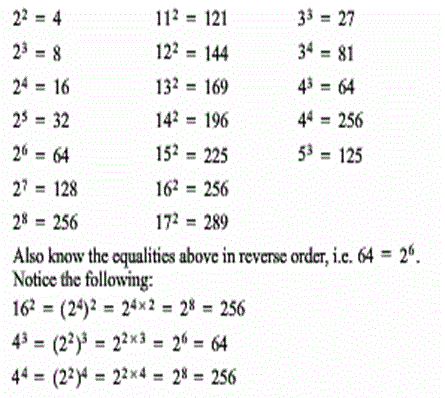
Other Numbers

Arithmetic
Order of operations

Fractions
Adding Fractions
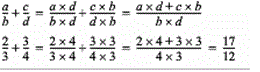
|
Subtracting Fractions
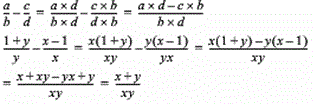
|
Multiplying Fractions

|
Dividing Fractions
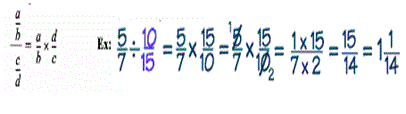
|
Dividing Exponents
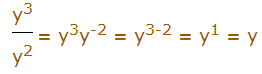
|
Multiplying small numbers
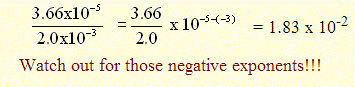
|
ALGEBRA
Simultaneous equations
The first step is to try to eliminate one of the unknowns. Here is an example of solving by substitution.
- Equation 1: 3x + y = 7
- Equation 2: 3x - 2y = 10
Using Equation 1 to write y in terms of x gives y = 7 - 3x. Plugging into equation 2 gives 3x - 2(7 - 3x) = 13. Solving x yields x = 3. Plugging in the expression for y gives y = -2.
One equation with two unknowns
Two unknowns can sometimes be solved in one equation under certain constraints.
- Ex: 9x + 5y = 52, with x and y as positive integers. Here, the only possible solution is x = 3, y = 5.
- Ex: Alex bought x headphones at $9 each and y earphones at $5 each, spending $52 in total. How many earphones did he buy?
We get the same equation 9x + 5y = 52. Be aware of that implicit assumption that x and y are positive integers.
Three Important Algebra Patterns
- Pattern #1: The Difference of Two Squares : A2 - B2=(A - B)(A + B)
- Pattern #2: The Squares of a Sum : ( A + B )2 = A2 + B2 + 2AB
- Pattern #3: The Squares of a Difference : ( A - B )2 = A2 + B2 - 2AB
What is the strategy for formula problems with unspecified amounts?
Ex: "The speed of the rocket was increased a certain amount.."
Pick smart (easy-to-work-with) numbers! (formula: change/original = %change)
What is the equation for linear sequences?
Sn = k(n) + x
Where k is the constant difference between successive terms.
x is the constant that determines S1 (must be solved for)